Einstieg in das Thema
Was brauchst du als Basiswissen?
Es ist sinnvoll, wenn du "K nächste Nachbarn" verstanden hast.
Worum geht es?
In "k nächste Nachbarn" testest du, zu welchem Bereich ein neues Element gehört. Die Einteilung der Gruppen war logisch, die Kriterien transparent. Und sie waren dir bereits gegeben.
Stell dir nun vor, du musst selbst eine Einteilung finden, und zwar erst einmal unabhängig von möglichen Eigenschaften. Darum geht es nun. Du siehst also eine Punktwolke und musst - zuerst durch Ansehen, später durch Berechnen - eine Einteilung finden.
Was ist das Ziel?
Du erkennst, dass ein System auch ohne große Interaktion von außen mit Daten umgehen - also mit diesen etwas lernen - kann.
Erarbeitung
Theorie
Aufgaben zur Orientierung
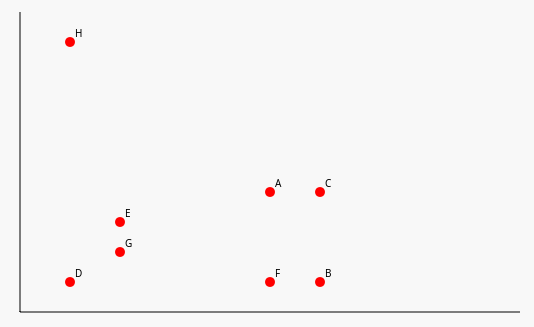
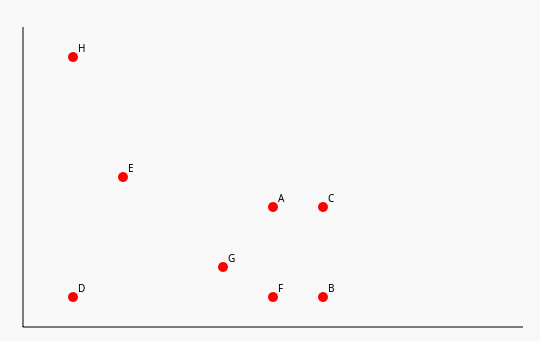

Theorie 2: Auf zum Algorithmus
Aufgaben zur Übung - eindimensional
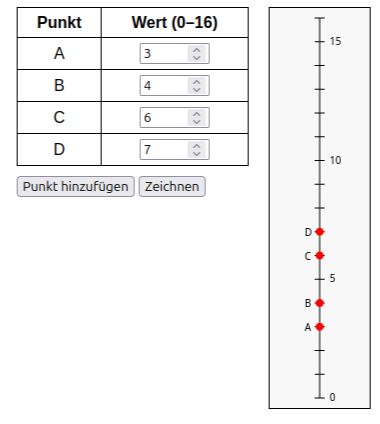
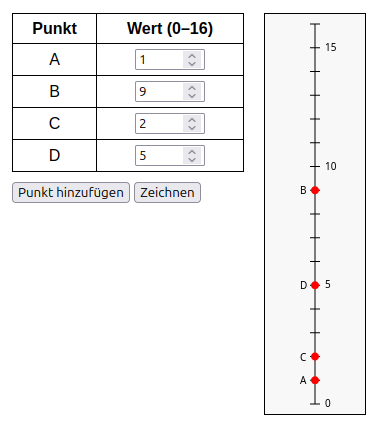
Aufgaben zur Übung - zweidimensional
Nun soll das Ganze zweidimensional erfolgen. Nutze dazu das
Kann man auch mehrere Gruppen machen? Na klar! Bei Anzahl der Cluster kannst du dies einstellen.
Komplexe Aufgabe ohne KI
Ohne obige Tools, aber gern mit Taschenrechner, kannst du die ersten beiden Schritte einer Zuordnung und die erste Schwerpunktberechnung durchführen. Damit kannst du zeigen, dass du das Verfahren verstanden hast.
Was muss man wissen/können?
Du weißt,
- dass man auf mathematischem Weg eine Punktwolke in Bereiche einteilen kann,
- dass man vorgeben muss, wie viele Bereiche (Cluster) man haben möchte und
- man sich ausrechnen lassen kann, wie gut die Einteilung passt.
Du kennst
- den Algorithmus,
- weißt, wie man beginnt und
- wann man stoppt.
Was können anschließende Themen sein?
Wir haben eine "flache Einteilung" vorgenommen, ein Punkt gehört entweder zu Cluster 1 oder zu Cluster 2. Man kann aber auch eine Hierarchie erstellen (lassen). Darum geht es jetzt.

