Einstieg in das Thema
Was brauchst du als Basiswissen?
Du kennst Graphen, weißt, was das ist und
erkennst sie.
Worum geht es?
Bis jetzt hast du dich mit den Grundlagen beschäftigt.
Das war mäßig aufregend. Spannend wird es ja
erst, wenn man auf den Graphen Algorithmen anwendet.
Wir beginnen mit dem guten Herrn Euler, der einst über
Brücken in Königsberg nachdachte.
Was ist das Ziel?
Am Ende kennst du Eulergraphen.
Erarbeitung
Aufgaben
Aufgabe 1
Günther muss Straßen überprüfen. Sind da Schlaglöcher, kaputte Verkehrsschilder, Müll auf der Straße usw. Er muss also jede Straße einmal abfahren und wieder dort ankommen, wo er losgefahren ist. Dabei muss das für jeden beliebigen Knoten als Start gelten! Überprüfe bitte, ob das bei folgenden Graphen möglich ist.
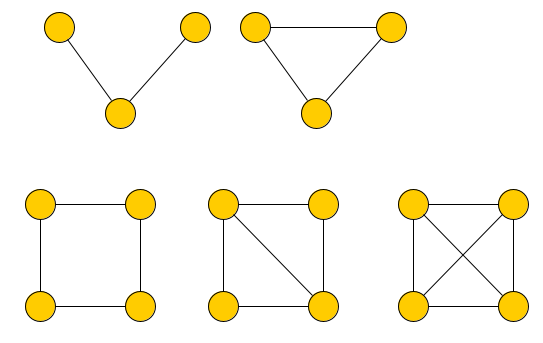
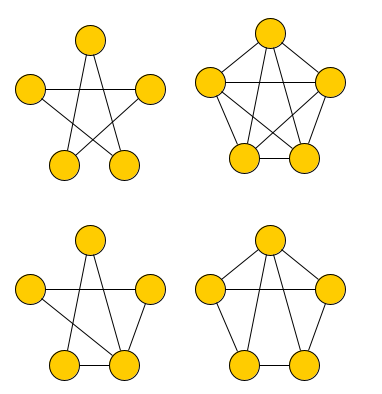
Aufgabe 2
Untersuche den Grad der Knoten bei allen Graphen der vorherigen Aufgabe, wo ein solcher Weg möglich ist. Schreibe alle Zahlen, die dabei als Grad vorkommen, auf.
Aufgabe 3
Schreibe nun ebenfalls alle Zahlen auf, die als Grad bei Graphen auftauchen, bei denen kein solcher Weg möglich ist.
Aufgabe 4
Stelle eine Vermutung auf, wie man erkennen kann, ob Graphen mit solchen Wegen (Start=Ziel, jede Kante einmal) durchlaufen werden können.
Nun müssen die Begriffe noch erarbeitet werden. Das Ziel ist,
Eulerweg, Eulergraph und Eulerkreis zu definieren.
Vervollständige die Aussagen. Die KI kann helfen.
Aufgabe 5
Wenn man jede Kante eines Graphen einmal durchlaufen wird, Start und Ziel aber nicht gleich sein müssen, dann spricht man von einem ............
Aufgabe 6
Wird jede Kante einmal durchlaufen und sind Start ............, dann spricht man von einem Eulerkreis.
Aufgabe 7
Enthält ein Graph einen Eulerkreis, so spricht man von einem ................
Aufgabe 8
Bei einem Eulerkreis sind die Grade der Knoten ..........
Nun kommt noch etwas Bekanntes:
Aufgabe 9
Ist das Haus vom Nikolaus ein Eulergraph, ein Eulerweg oder nichts von beidem?
Vertiefung
Bisher haben wir ungerichtete Graphen untersucht.
Wie aber ist das bei gerichteten Graphen? Hier sind wieder
ein paar Beispiele, die du analysieren sollst.
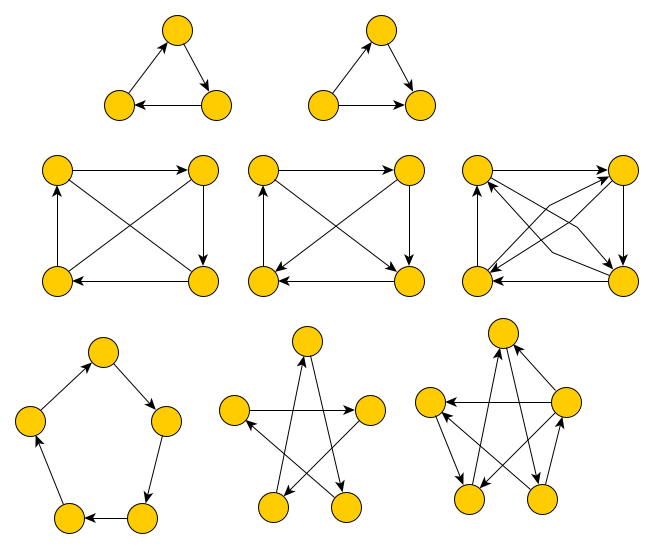
Aufgabe 10
Untersuche alle Graphen. Bei welchen ist ein Eulerkreis möglich?
Aufgabe 11
Untersuche die Zahl eingehender und ausgehender Kanten bei diesen Graphen. Schreibe sie auf.
Aufgabe 12
Stelle eine Vermutung auf, wann ein gerichteter Graph ein Eulergraph ist.
Zusammenfassung
Was muss man wissen/können?
Du weißt,
- was ein Eulergraph ist,
- welche Bedingungen für ihn gelten und
du kannst
- Eulergraphen erkennen und
- auch selbst konstruieren.
Was können anschließende Themen sein?
Das war das erste Kapitel zum Durchlaufen eines Graphen.
Es gibt aber noch viel mehr. Erkunden wir nun
Höhlensysteme.



